Formal Fallacies

Formal Fallacies

Formal fallacies are deductively invalid arguments that typically commit an easily recognizable logical error. Formal fallacies are also called structured fallacies, as they arise due to errors in facts or reasoning. These fallacies can be identified if we explain why these arguments are invalid even for a single instance.

In this chapter, we shall discuss five types of formal logical fallacies.

1. Subset Arguments
2. Modus ponens 
3. Modus tollens
4. Hypothetical Syllogism
5. Disjunctive Syllogism

1: Subset Arguments

An argument is valid if the conclusion follows the premises. 

• All A are B
• All B are C
• Therefore, All A are C

We can express the Subset Argument in the form of the following Vein Diagram.  

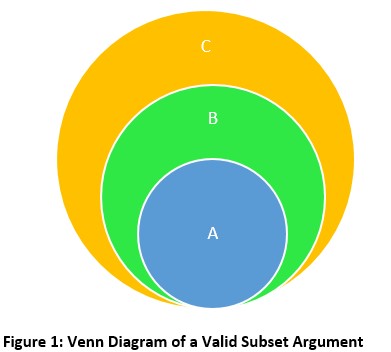
In natural language, an example of subset argument is

• All women are humans
• All humans are mammals
• Therefore, all women are mammals

It can be seen from the Venn Diagram that if the premises are correct, the conclusion can’t be false. However, if we are not careful, we may make errors in the argument and reach the wrong conclusion. For instance, the following shall be an invalid argument

 Invalid Argument

• All A are B
• All C are B
• Hence, all A are C

The Venn Diagram of the above argument can be shown as follows.

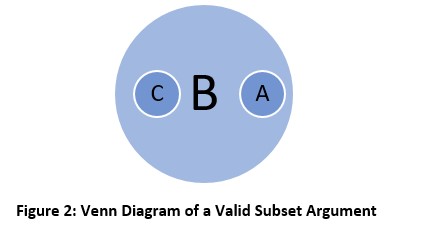
In natural language, the argument can be presented as follows.

Invalid Argument

• All men are humans
• All women are humans
• Hence, all men are women

The above argument is clearly invalid as the premises do not lead to the conclusion that all men are women.

2: Modus ponens (IF-THEN arguments)

It is a mode of reasoning from a hypothetical proposition according to which if the antecedent be affirmed, the consequent is affirmed. It means that if one thing is true, then another will be.  It can be represented in the following form.

Valid Argument

• If A then B
• A is true,
• Then B is True

In common language, an example of such an argument is,

• If John is murdered, John is dead
• John is murdered.
• So, John is dead.

However, it is important to note that If A implies B, then the reverse is not necessarily implied.  It means that affirming the consequent does not make the antecedent valid.

Invalid Argument

• If A, then B
• B is true,
• Then A is True

In common language, 

• If John is murdered, John is dead
• John is dead
• So, John is murdered

Unless you are careful, you may tend to agree with the conclusion of the above argument, though it is invalid. Hence, it is a good example of a logical fallacy. However, to establish the above argument as a fallacy, we need one example to establish that either the truth or logic conditions are invalid. This is not a valid argument since John may not have been murdered but could have died of any other reason, like illness, accident, etc. Let’s take another argument.

Argument

• P: If a person is allergic to peanuts, he does not eat peanut butter.
• P: John does not eat peanut butter.
• C: John is allergic to peanuts.

For instance, in this case, assuming that the premises are correct, the conclusion can be wrong. For instance, John may not eat peanut butter because he does not like the taste of butter. Hence, just because John does not eat peanut butter does not mean that John is allergic to peanuts. Hence, the argument is invalid. However, some people won’t understand the error in logic and may get convinced by the argument.

3: Modus Tollens

Modus tollens (MT) arguments have the same first premise as with modus ponens, but the denial of the second premise leads to the conclusion that the first part of the premise should be denied as well.

Its logical form is as follows.

• If A, then B
• Not B
• Therefore not A.

In common language, the argument can be expressed as following.

• If you have a PhD, then you are a graduate
• You are not a graduate
• Therefore, you don’t have a PhD.

While denying the consequent implies denial of the antecedent, the reverse is not true. Hence, the following argument shall be invalid.

• If A, then B
• Not A
• Therefore, not B.

In common language 

• If you have a PhD, then you are a graduate
• You don’t have a PhD
• Therefore, you are not a graduate.

This argument is clearly wrong because you first become a graduate and then go for a PhD. Hence, not having PhD does not mean that you are not a graduate.

4: Hypothetical Syllogism 

 In a Hypothetical Syllogism, both the premises and the conclusion are conditional statements. The antecedent of one premise must match the consequent of the other for the conditional to be valid. The structure of Hypothetical Syllogism can be expressed as follows.

• If A, then B.
• If B, then C.
• Therefore, If A, then C.

In a simple language, we can present the argument as follows,

• If I want a government job, then I need to pass the examination.  
• If I need to pass the examination, I must study.  
• Therefore, if I want a government job, I must study.

However, the relationship flows in one direction only, and the opposite is not a valid argument.  Hence, the following argument is not valid.

• If not A, then not B.
• If not B, then not C.
• Therefore, If not C, then not A.

Hence, the following argument shall be invalid.

• If I  don’t want a government job, then I don’t have to pass the examination.  
• If I don’t have to pass the examination, I  don’t have to study.  
• Therefore, if I don’t want a government job, I  don’t have to study.

The argument is invalid because even if you don’t want a government job, you still have to study to get a private job or to acquire new knowledge and skills.

5: Disjunctive Syllogism (OR)

Disjunctive Syllogism includes ‘OR’, which means either the first or second or the third, or the nth.  If even one of them is present, the argument shall be valid.

Two alternative arguments can be presented as follows.

• Either A or B
• Not A.
• Therefore, B

Similarly, a three alternative argument can be as follows.  

• Either A or B or C
• Not A
• Not B
• Therefore, C

An example of valid Disjunctive Syllogism is as follows.

• John is either in the office or at home
• John is not in the office
• Therefore, he is at home

The following argument is also valid.

• The college teacher must have either a Masters or a PhD
• The college teacher does not have a PhD
• Therefore, he has the Master’s degree

However, the following Disjunctive Syllogism shall be invalid.

• Either A or B
• A
• Therefore, Not B

However, the above argument is valid only if OR is exclusive, meaning there is nothing common between A and B. Accordingly, the following argument shall be invalid. 

• The college teacher must have either a Masters or a PhD
• The college teacher has a master’s degree
• Therefore, he is NOT a PhD

The above argument fails since a PhD usually includes a Master’s degree. Hence, a above structure of a disjunctive syllogism is valid only when both alternatives are mutually exclusive.

The appropriate argument, which can be valid even in both the inclusive and exclusive cases, can be expressed as follows.

• Either A or B
• not-A
• Therefore, B

In some institutes, a Masters degree is not a requirement for a PhD. For instance, in India, you can enrol for the PhD directly after your BE or B Tech. However, the above structure of the argument is always valid. For example, if the teacher does not have a PhD, he must have a Master’s degree. However, if he does not have a Master’s degree (because a Master’s degree was not mandatory for a PhD), he will surely have a PhD.

Take the Test